다이나믹 프로그래밍(=동적 계획법)
- 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법
- 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 함
- 한 번 해결한 문제는 다시 해결하지 않도록 함
- 탑다운(하향식) / 보텀업(상향식)으로 두 가지 방식으로 구성
- 다이나믹 프로그래밍의 다이나믹은 별다른 의미 X
( * 자료구조에서 사용하는 동적 할당(프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법)과는 다름 )
다이나믹 프로그래밍의 조건
다음의 조건을 만족할 때 사용할 수 있음
1. 최적 부분 구조(Optiaml Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음
- 큰 문제를 작은 문제로 나눌 수 있음
2. 중복되는 부분 문제(Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야함
파보나치 수열
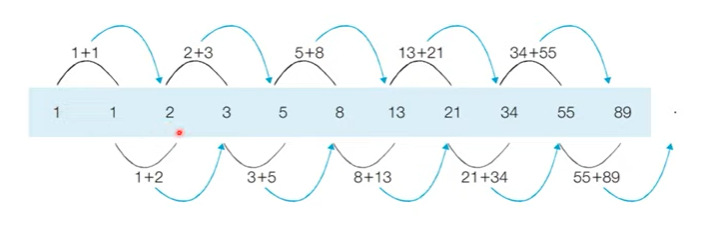
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
점화식 : 인접한 항들 사이의 관계식
피보나치 수열의 점화식

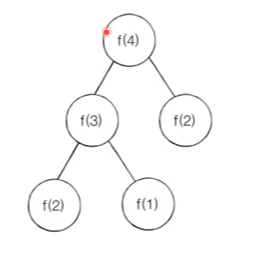
피보나치 수열 : 단순 재귀 소스코드
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(4))
피보나치 수열(단순 재귀 함수 이용) 시간 복잡도
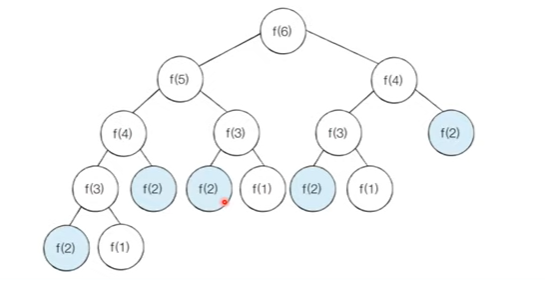
단순 재귀 함수로 피보나치 수열을 해결하게 되면 지수 시간 복잡도를 가짐
특정 함수가 여러번 호출되는 것을 확인 할 수 있음 -> 중복되는 부분 문제
메모이제이션(Memoization)
- 한 번 계산한 결과를 메모리 공간에 메모
- 같은 문제를 다시 호출하면 메모했던 결과 가져옴
- 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 함
탑다운 VS 보텀업
- 탑다운(메모제이션) : 하향식
- 보텀업 : 상향식
- 다이나믹 프로그래밍의 형태는 보텀업 방식
- 결과 저장용 리스트는 DP 테이블
- 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 개념
- 다이나믹 프로그래밍에 국한된 개념이 아님
- 한 번 계산된 결과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수 있음
탑 다운 방식 다이나믹 프로그래밍 (시간 복잡도 = O(N))
#다이나믹 프로그래밍
#탑다운 방식(하향식, 메모제이션)
#한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100
def fibo(x):
if x == 1 or x == 2:
return 1
#이미 계산한 적 있는 문제라면 그대로 반환
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))보텀 업 방식 다이나믹 프로그래밍
d = [0] * 100
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n+1):
d[i] = d[i-1] + d[i-2]
print(d[n])다이나믹 프로그래밍 VS 분할 정복
다이나믹 프로그래밍과 분할 정복 모두 최적 부분 구조를 가짐
- 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제를 해결
다이나닉 프로그래밍과 분할 정복의 차이점 = 부분 문제의 중복
- 다이나믹 프로그래밍 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복됨
- 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산 X
퀵 정렬의 예시
- 한 번 기준 원소(피벗)가 자리를 변경해서 자리를 잡으면 그 원소의 위치는 바뀌지 않음
- 분할 이후에 해당 피벗을 다시 처리하는 부분 문제는 호출하지 않음
다이나믹 프로그래 문제 접근 방법
- 주어진 문제가 다이나믹 프로그래밍 유형임을 파악
- 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는 지 검토
- 다른 알고리즘 풀이 방법이 떠오르지 않는다면 다이나믹 프로그래밍 고려
- 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 사용
#1. 문제 ) 개미 전사
위 문제가 다이나믹 프로그래밍 문제와 성립되는지 확인
> 최적부분 구조와 중복되는 부분 문제의 조건이 성립되는가?
최적부분 구조 : 특정 번째 까지의 최적의 해를 이용해서 계산될 수 있음 (큰 문제를 해결하기 위해 작은 문제를 이용함)
중복되는 부분 문제 : 점화식을 통해 표현할 수 있으며 이는 동일한 작은 문제를 반복적으로 해결해야 함
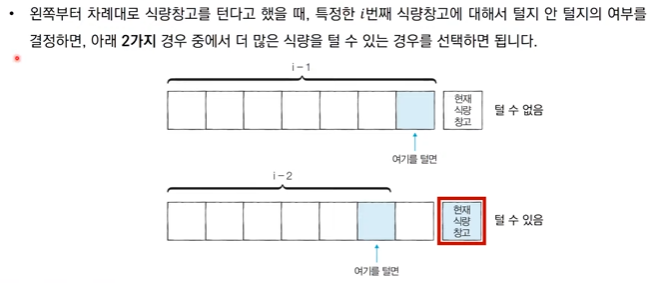
1 ) N = 4일때, 식량을 선택할 수 있는 경우의 수는 8가지

2 ) ai = i 번째 식량창고까지의 최적의 해(얻을 수 있는 식량의 최댓값)

# 개미전사
n = int(input())
array = list(map(int, input().split()))
d = [0] * 100
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
d[i] = max(d[i-1],d[i-2]+array[i])
# 계산된 결과 출력
print(d[n-1])#2. 문제 ) 1로 만들기

x = int(input())
d = [0] * 30001
def counting(x):
for i in range(2, x+1):
d[i] = d[i-1] + 1
if d[i] % 2 == 0:
d[i] = min(d[i], d[i//2]+1)
if d[i] % 3 == 0:
d[i] = min(d[i], d[i//3]+1)
if d[i] % 5 == 0:
d[i] = min(d[i], d[i//5]+1)
return d[x]
print(counting(x))#3. 문제 ) 효율적인 화폐 구성
n, m = map(int, input().split())
cost = list(int(input()) for _ in range(n))
# 한 번 계산된 결과를 저장하기 위한 dp 테이블
d = [10001] * (m+1)
# 다이나믹 프로그래밍 진행(보텀업)
d[0] = 0
for i in range(n):
for j in range(cost[i], m+1):
if d[j - cost[i]] != 10001: # (i-k)원을 만드는 방법이 존재하는 경우
d[j] = min(d[j], d[j-cost[i]]+1)
# 계산 결과 출력
if d[m] == 10001: # 최종적으로 m원을 만드는 방법이 없을 경우
print(-1)
else:
print(d[m])#4. 문제 ) 금광 문제
testcase = int(input())
for tc in range(testcase):
n, m = map(int, input().split())
array = list(map(int, input().split()))
dp = []
index = 0
for i in range(n):
dp.append(array[index:index+m])
index += m
print(dp)
for j in range(1, m):
for i in range(n):
if i == 0:
left_up = 0
else:
left_up = dp[i-1][j-1]
if i == n-1:
left_down = 0
else:
left_down = dp[i+1][j-1]
left = dp[i][j-1]
dp[i][j] = dp[i][j] + max(left_up, left, left_down)
result = 0
for i in range(n):
result = max(result, dp[i][m-1])
print(result)#5. 문제 )
n = int(input())
bung = list(map(int, input().split()))
bung.reverse()
dp = [1] * n
for i in range(1, n):
for j in range(0, i):
if bung[j] < bung[i]:
dp[i] = max[dp[i], dp[j + 1]]
print(n-max(dp))
'Algorithm' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 - 크루스칼 알고리즘 (0) | 2022.05.24 |
|---|---|
| [알고리즘] 서로소 집합 (Disjoint Sets) (0) | 2022.05.24 |
| [알고리즘] 이진 탐색 알고리즘 (0) | 2022.05.06 |
| [알고리즘] 정렬 알고리즘(Sorting)(3) - 계수 정렬 (0) | 2022.05.06 |
| 정렬 알고리즘(Sorting)(2) - 퀵 정렬 (0) | 2022.05.06 |



